
Research
The theme that best captures the various research projects in our group is the study of collective dynamics phenomena in living systems, ranging from the interactions of many proteins at the nanoscale to many organisms at the population level. We predominantly use theoretical models and simulations to study these systems, though always in close collaboration with experimental groups. At present, we pursue three active lines of research: collective dynamics of self-propelled particles, collective dynamics of membrane-embedded proteins through membrane-mediated interactions, and the role of mechanics in early embryo development.
Collective dynamics of active soft particles
Collaborators:
Seraphine Wegner (Münster)
Rinke van Tatenhove-Pel (TU Delft)
Sander Tans (TU Delft/AMOLF)
References:
Phys. Rev. E 91, 032706 (2015) / arXiv:1411.4821
Traffic and Granular Flow '15 (2015)
EPL 125, 36001 (2019) / arXiv:1611.09125
arXiv/2003.10509 (2020)
arXiv/2103.04312 (2021)
Advanced Science 11, 2310079 (2024)
ISME Comm. 5, ycaf004 (2025)

Soft particles are particles that can deform when they touch each other, resulting in a finite repelling force (rather than an infinite one, which is the case for hard particles). Both soft and hard particles undergo a jamming transition when their density gets above a certain critical value. When jammed, the particles have no degrees of freedom and thus can not move. We are interested in the case that the particles are self-propelled, which may both cause them to become jammed more quickly, and help them to break up a jammed cluster. To study this system, we use Brownian-dynamics like simulations as well as analytical techniques.
In our simulations, we use only local interaction rules, based on interactions with neighbouring particles, tendencies to align with local velocity fields, and boundary effects (e.g. wanting to go into a group when on the edge). From these, we find different kinds of behaviour, such as collective diffusive migration and torus formation. The type of behaviour we obtain is not only set by the interaction parameters, but also by the group size - so even though the rules are local, global variables still can determine the resulting patterns.
In collaboration with groups in Delft, Leiden and AMOLF, we apply our simulations to a range of real-life systems, ranging from macroscale beetles to microscale amoebas.
Membrane-mediated interactions
Group people:
Pietro Sillano
Haochun Sun
Collaborators:
Gijsje Koenderink, Cees Dekker, Marileen Dogterom (TU Delft)
Daniela Kraft (Leiden Institute of Physics)
Anđela Šarić (IST Austria)
References:
Phys. Rev. Lett. 104, 198102 (2010)
Scientific Reports 6, 32825 (2016) / arXiv:1603.04644
Phys. Rev. Lett. 117, 138102 (2016) / arXiv:1510.03610
Soft Matter 13, 4924-4930 (2017) / arXiv:1703.00776
eLife 6: e30292 (2017).
Curr. Opin. Colloid Interface Sci. 40, 58-69 (2019)
Soft Matter (2021) / doi:10.1039/D0SM01758B
Phys. Rev. E 106, 024401 (2022)
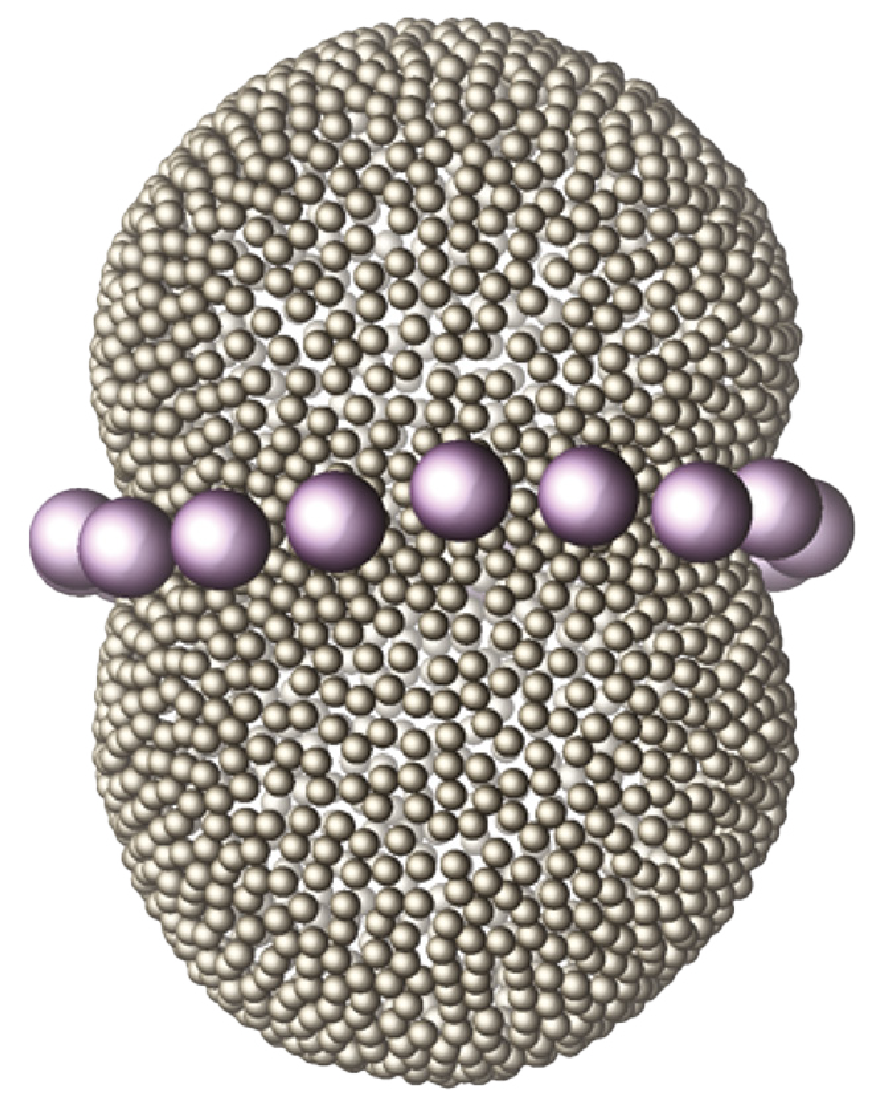
All biological membranes consist of two components: a bilayer of lipids (blue particles in figure on the right) and membrane-associated proteins (schematically indicated by the red triangles). The lipids have hydrophilic heads and hydrophobic (oil-like) tails, which causes them to self-organize into bilayers in water. Becuase the lipids are roughly cylindrical in shape, these bilayers can be large, and essentially form a continuum of lipids, that act as a two-dimensional fluid. Proteins with a hydrophobic part may embed in that bilayer and become integral part of the membrane. Through their functionality, the proteins also turn the membrane from a passive barrier to an active component of the cell or organelle it encloses. Proteins come in a rich variety of shapes. If they are not the same size and cylindrical shape as the membrane, they will locally deform the lipid bilayer to match their particular shape, such as the cones in the image. Much like two heavy balls on placed a mattress will attract each other through deforming the mattress, two protein inclusions will interact through the deformations they impose on the membrane. We study these interactions, in the setting of both flat and strongly bent membranes, and investigate how the membrane mediated interactions between the proteins drive cellular processes like tube and vesicle formation and membrane fission.
Mechanics of tissue development
Collaborators:
Maurijn van der Zee (Institute of Biology, Leiden)
Stefan Semrau (Leiden Cell Observatory)
Chirlmin Joo (TU Delft)
References:
Phys. Rev. E 89, 062709 (2014)
J. Theor. Biol. 454, 182-189 (2018) / arXiv:1705.06205
J. Tissue Engineering 13, 20417314221103042 (2022)

We study the properties of developing eukaryotic tissue from a mechanical perspective. To do so, we developed our own tissue model, treating the nucleus as a passive tracer, and the actin/membrane cortex as an active material.
Mechanics of early embryo development
Early Drosophila mitotic waves
Collaborators:
Julien Dubuis, Thomas Gregor (Princeton University)
Lisa Manning (Syracuse University)
Louis Kang, Philip Nelson, Tom Lubenksy, Andrea Liu (UPenn)
References:
Eur. Biophys. J. 42, 647-654 (2013)
PLoS ONE 8, e77216 (2013)
Phys. Rev. E 89, 062709 (2014)


During the early stages of development of Drosophila embryos (the first 13 divisions), most nuclei populate the same cytosol without being divided into seperate cells by membranes. These nuclei are known as the syncytial nuclei. They populate the bulk of the embryo for cell divisions 1-8, after which most of them migrate to the surface, where we can visualize them by staining e.g. the histone in their DNA (see the site of the Gregor lab for movies). Using newly developed algorithms, we track the positions and shapes of the nuclei over time as they divide and form families of daughter nuclei. We find that the divisions occur in waves, originating from the embryo's poles, Studying the motion and shapes of the nuclei gives us a direct, non-penetrative handle on the dynamics inside the developing embryo, which allows us to study their mechanical properties in vivo. Moreover, we can combine these observations with simultaneous measurements of protein gradients, for example Bicoid, which is responsible for anterior-posterior symmetry breaking in the embryo. Doing so, we find emerging collective behavior, resulting from the local behavior at the level of the single nuclei.
Early chicken hearttube beating
Collaborators:
Stephanie Majkut, Dennis Discher, Andrea Liu (UPenn)
References:
Curr. Biol. 23, 2434-2439 (2013)
Phys. Rev. E 89, 062709 (2014)
The first organ a chicken embryo builds is a simple heart tube, which will later grow into the complete heart with four chambers. From very early on, this embryonic heart is beating, pumping blood around by contracting in a wavelike fashion. To sustain such a wave in a heavily overdamped environment, each individual cell has to contribute energy and amplify the signal, not just to contract the heart but also to keep the wave going at all. We study how the wave propagation depends on the mechanical properties of the tissue, as well as the interaction between the contracting elastic heart tube and the viscous blood that it pumps around.
Membrane shape and composition
Membranes are everywhere in living cells - they form the boundary layer between the cell and its surroundings, and also the boundaries of the various organelles within the cell. Biological membranes are bilayers of ampiphilic lipids, which have both a hydrophilic part (a polar head group) and a hydrophobic part (one or more fatty acid tails). They make an interesting physical system as well, as they behave like a (two-dimensional) liquid within the plane of the membrane, whereas when bending a membrane in its normal direction, it behaves like an elastic solid. In biological systems, membranes moreover are home to many proteins, whose very presence influences both the shape and the dynamics of the membrane.
Shapes of multi-component membranes
Collaborators:
Stefan Semrau, Thomas Schmidt (Leiden University)
Cornelis Storm (TU Eindhoven)
References:
PRL 100, 088101 (2008)
Biophys. J. 96, 4906-4915 (2009)
PRL 104, 198102 (2010)
EPJE 34, 67 (2011)
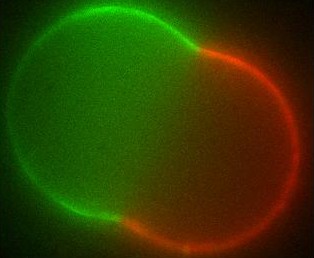
The different membranes found in living cells exhibit a broad range of chemical compositions as well as a rich variety of (sometimes exotic) shapes. Over the last decades there has been a vivid discussion in the biophysics community as to whether the different molecules that make up the cell membrane (generically known as lipids) are organized into domains (called rafts) within the membrane or not. Such domains, if they exist in living cells, are too small to observe by optical microscopy; in artificial systems though, they can grow large and have indeed been seen.
Using differential geometry, we have developed a model for the shape of artificial membrane vesicles, which takes several properties of the membrane as parameters. Some of these can be measured directly, the remaining ones can now be obtained by fitting this model to the actual shapes, which we do in collaboration with the experimental biophysics group. The numbers we get out can be applied to living cells to determine conditions for domains to exist there and decide on which biological processes may be involved.
The large domains found in biomimetic vesicles also allow us to study curvature effects and membrane-mediated interactions between domains, comparable to the forces felt by proteins in living cells. These interactions can be quantified experimentally as well. We model them by again considering the effect the domains have on the curvature of the surrounding membrane. From this model we can explain both the measured interaction strengths and observed domain size distribution. Moreover, we find that the interaction has a striking effect: due to its nonlinearity, it spontaneously sorts membrane inclusions by size.
Phase diagrams of ternary lipid systems
Collaborators:
J. M. J. van Leeuwen (Leiden University)
Cornelis Storm (TU Eindhoven)
References:
Phys. Rev. E 80, 041924 (2009)
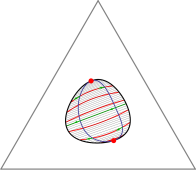
The Gibbs phase triangle (a section through the phase diagram at constant temperature and pressure) of a ternary lipid system exhibits a rich variety of phase coexistence regimes. Lipid mixtures can be in one of two liquid phases and a gel phase, and all of these can coexist, in pairs or even all three together. Especially intriguing is the recent discovery that there are systems for which each of the three underlying binary mixtures is uniform at a given temperature and pressure, but the ternary system exhibits phase separation. Extending Flory-Huggins theory for binary systems, we have developed a model that can explain all these different phase diagrams. Moreover, we can use our theory to predict the behavior of the line tension between coexisting phases as we move through composition space.
Molecular motors
Collective behaviour of nonprocessive molecular motors
Collaborators:
Paige Shaklee, Thomas Schmidt (Leiden University)
Marileen Dogterom (AMOLF)
Cornelis Storm (TU Eindhoven)
References:
PNAS 105, 7993-7997 (2008)
Biophys. J. 99, 1835-1841 (2010)
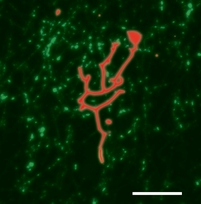
Molecular motors are the workers of the cell. They are the ones responsible for all transport processes, which can not rely on simple diffusion because it would be too slow. Molecular motors can 'walk' along the cell's 'roads' and 'highways' (the actin and microtubule networks) and increase distribution speeds to the necessary level. Moreover, motors also pull on the cell membrane and help create and maintain the non-equilibrium shapes of organelles such as the endoplasmic reticulum and the Golgi apparatus. Some motors, like Kinesin, are very efficient: a single one can take many steps along a microtubule before unbinding, and only a few are needed to transport a small vesicle from the nucleus to the cell perifery. However, there are also less efficient, so-called nonprocessive motors which unbind after taking only a single step. Amazingly, both types can pull membrane tubes, though the mechanism is quite different. Kinesin has been shown to dynamically cluster at the tip of a tube, where they cooporate to produce the necessary force to extract the tube from its mother vesicle. We have shown that, as part of this clustering process, kinesin motors get constantly recycled during tube pulling. Nonprocessive motors like Ncd on the other hand are a lot more dynamic. We found that these motors can create oscillating tubes, allowing for length regulation and exploration of different cell regions.
Hydrodynamics
Self-diffusiophoresis
Collaborator:
Gareth Alexander (Warwick University)
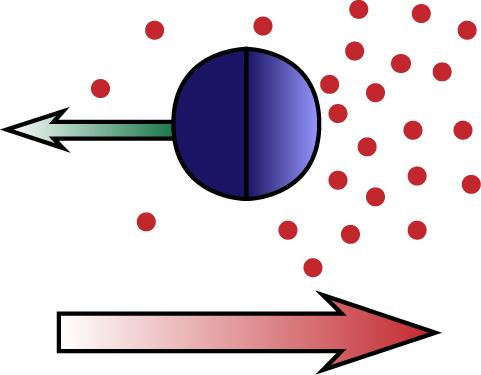
Diffusiophoresis is the process by which particles move trough a chemical concentration gradient, due to an attractive or repulsive interaction between the particle and the chemical compound. In self-diffusiophoresis the particle itself produces the compound it interacts with. An example is a particle that catalyzes the reaction 2H2O2 → 2H2O + O2, creating an O2 gradient and interacting with it. Another example is a particle that facilitates the polymerization of a biopolymer (e.g. actin), which creates a gradient because individual monomers diffuse, whereas the polymers do not. The latter process is one possible mechanism for the propulsion of Lysteria bacteria by means of actin 'comet tails'. We study these and related processes, analytically solving the Stokes equation for the fluid flow and extracting the particle motion in the diffusion dominated and advection dominated limits.
Flows in dividing cells
Collaborators:
Ed Banigan (Northwestern University)

During cell division, two sets of chromosomes are dragged through the cell to opposite ends. Chromosome separation is an active and highly nonequilibrium process, in which the cell generates large forces mediated by mitotic spindles. Consequently, the process of cell division also generates large fluid flows that extend over the entire volume of the cell, and potentially help with the separation. We study these flows analytically in the zero Reynolds number limit, solving the Stokes equation for a fluid contained in a membrane shell.
Cell adhesion
Cell adhesion and tumorigenesis
Collaborators:
Collaboratiors: Markus Basan, Martin Lenz, Thomas Risler, Jean-François Joanny (Institut-Curie, Paris, France)
References:
Biophys. J. 98, 2770-2779 (2010)

When epithelial cells are placed on an elastic substrate and are given sufficient amounts of nutrients, they will grow along the substrate by extending filopodia. The force necessary for pushing the filopodia outward is provided by actin polymerization in the direction perpendicular to the cell's plasma membrane. During this growth stage the actin constantly grows and shrinks, and moreover branches and builds a network. When the cells have produced a confluent layer, the growth direction switches from parallel with to perpendicular to the membrane, until the cells mature at a height that depends on their specific type. The actin then no longer pushes on the membrane but instead forms a belt near the apical side of the cell. It reorients itself to be parallel to the membrane and forms bundles instead of branches. We investigate the process by which cells 'feel' the presence of a neighbor and switch from a growing state to a mature equilibrium state. Using reaction-diffusion systems, we study the role of several transmembrane and cytoplasmic proteins in this contact inhibition process, and also consider the possible ways in which it can go wrong, resulting in cancerous cell growth.